What are possible shapes of tiles, if you would like to regularly cover a floor without gaps and overlappings? A mathematical theorem states, that this can only be achieved with basic shapes which have a 1-,2-,3-,4- or 6-fold symmetry. However, with the Penrose Puzzle you can cover a plane with a pattern of figures with 5-fold symmetry. The pattern is irregular and can theoretically be continued to infinity. There is a special trick: The Penrose Puzzle uses two different basic elements.

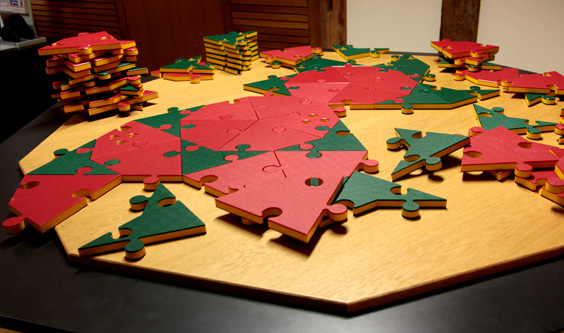
Put the pieces of the puzzle together so that the table is completely covered. Due to the shape of the table, you will not because a once recognized pattern can not be simply repeated. The finished puzzle shows an irregular pattern, in which different symmetrical figures appear again and again.